Photosynthesis, respiration and transpiration are important physiological processes for the survival and growth of green plants. Most of these physiological processes take place over the leaf surface. The leaf area index as the size of the green plant leaf area per unit area is an important indicator reflecting the total area of ​​the photosynthetic, respiratory and transpiration processes of the ecosystem. The leaf area index is directly related to many important ecological parameters such as ecosystem evapotranspiration, total primary productivity, and interception of canopy light. Therefore, leaf area index is an important input parameter in some models of productivity and evapotranspiration. .
Methods for measuring the leaf area index of forests include live leaf area metering and optical instrumentation. The single leaf area of ​​broad-leaved trees is relatively easy to measure either directly or using instruments. There are also many reports related to leaf area index, and coniferous leaves are relatively difficult to measure directly. Therefore, the direct measurement method is used in the study of early leaf area index. More. With the deepening of research and the appearance of various measuring instruments, there have been reports of the use of instruments (canopy analyzers, etc.) to measure the leaf area index of needles. However, most of the instruments used to measure the leaf area index have a premise that they are assumed to be randomly distributed in the canopy space. This condition can only be established when the stand density is high. Moreover, the evergreen conifers have a leaf age of more than 1 year. Because of the different leaf ages, there are certain differences in photosynthetic characteristics and specific leaf area. However, instrumental methods cannot distinguish between perennial and current-year leaves. In the report of the direct measurement method used to study the leaf area index of pine plants, most of the conifers are assumed to be cylinders approximately. However, whether they are cylindrical or not is yet to be studied.
Although not native to China, wetland pine is widely introduced in China because of its adaptability, poor tolerance, ability to produce resin, and other characteristics. Pinus elliottii belongs to the evergreen tree species. According to the author's observation, the leaf age is up to 4 years. There are two types of leaves, one with two needles and one with three needles. This paper proposes to use traditional measurement methods to explore the reliability of calculating the leaf area of ​​each pine wet leaf as a cylinder, study the relationship between the leaf length and leaf area of ​​the wetland pine, and compare the differences in specific leaf area of ​​different types of leaves. Using plot survey data and standard wood data to calculate the leaf area index of Pinus elliottii at the Qianyanzhou Experimental Station, provide comparative data for instrumental measurements and provide basic parameters for clarifying the productivity characteristics of plantation.
1 Material Methods
1.1 Sample Site Profile
The research site is the core experimental area of ​​the Qianyanzhou Experimental Station of the Chinese Academy of Sciences. It is located in Guanxi Township, Taihe County, Jiangxi Province, with longitude 115°04′13′′ east longitude and 26°44′48′′ north latitude. The altitude of the test area is about 100m and the relative height is 20~50m. It is a typical red soil hilly landform. The average annual temperature in the test area is 17.9°C,≥0°C active accumulated temperature is 6523°C, the average annual precipitation is 1489mm, precipitation is concentrated in April to June, and in July and August, the temperature is less and less rain, and it is prone to fall and fall drought; the sunshine duration is 1406h, the annual sunshine The percentage is 43%. The total annual solar radiation is 4349MJ/m2. The frost-free period is 323d. It has typical subtropical monsoon climate characteristics. The main soil type is red soil. The parent material of soil is mostly red sandstone, glutenite or mudstone and river alluvium. The type of land use is mainly planted forest, and the afforestation time is around 1984. The main tree species are Pinus elliottii, Pinus massoniana and Chinese fir.
1.2 Research Methods
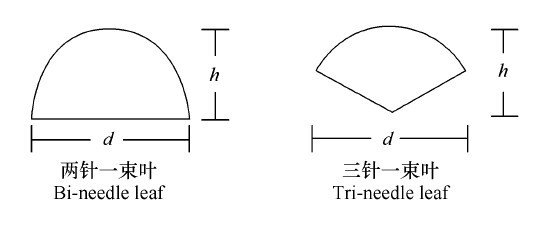
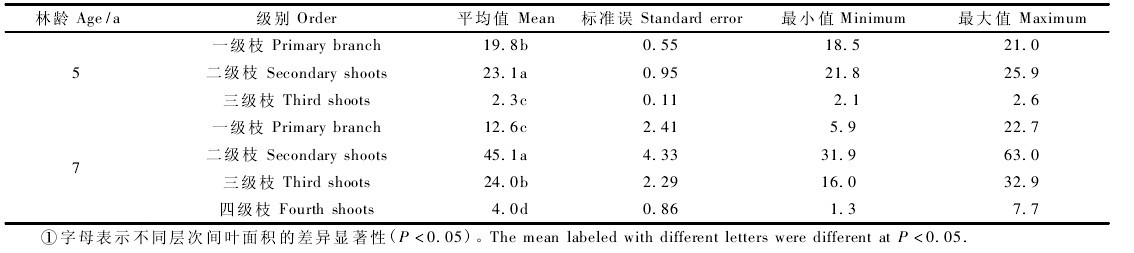
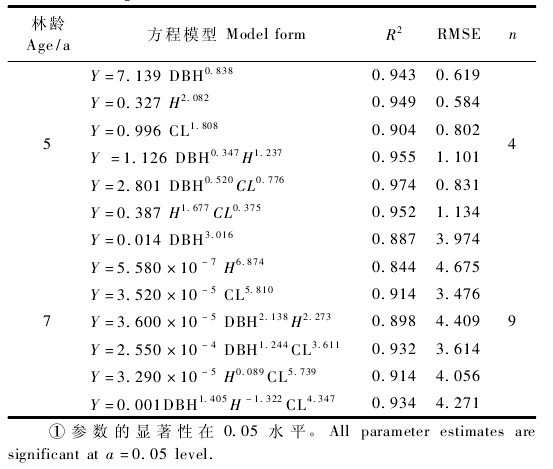
In August 2003, four pine weeds were cut, and 156 healthy shoots were taken. Each perennial leaf and each year's leaves were weighed. The water content was sampled and converted to dry weight. The perennial leaves were calculated. The percentage of annual leaves and the regression relationship between shoot base diameter and total leaf biomass were combined to calculate the leaf biomass of these fallen trees in combination with the measurement results of the diameters of the branches of 15 snow fallen trees to establish a single wood DBH of the wetland pine, The functional relationship between tree height and leaf biomass. At the same time, sample plots of the wetland pine forest at the test station were surveyed, and two 20m×20m sample plots were made for each wooden inspection scale. In August 2004, a portion of the perennial loose leaf and the current year's leaf were randomly selected and sampled to determine the moisture content. At the same time, two needles, one bunch of perennial leaves, eight bunches of leaves, and nine bunches of leaves of the year and twelve bunches of perennial leaves were taken. Annually 11 leaves, each needle using a 1/100 electronic balance to weigh fresh weight and use a steel tape measure the length of each leaf (l), using digital display vernier caliper (precision 0.01mm) to measure the leaf length 1/4, 1 The widths (d) and thicknesses (h) at /2 and 3/4 were three times each, and the average was taken as the width and thickness at that point. The average of the three averages was calculated as the width and thickness of the blade. Using a precision chemical instrument such as a burette to measure the volume of each blade according to the principle of drainage, calculate the diameter of each needle as a cylinder and compare it with direct measurement data. In March 2005, 10 trees were surveyed, and the percentage of each year in each branch of each tree was selected to investigate two needles and one leaf and three needles and one leaf. In August 2005, some two-needle bundles and three-needle bundles of blades were taken for freehand slicing. After scanning with a resolution of 1200 dpi, image processing software was used to measure parameters such as blade width, thickness, perimeter, and cross-sectional area to determine the shape of the blade. evidence. The statistical test method used in the article is written by Tao Tao, "Applied Mathematical Statistics Method."
2 results
2.1 Determination of leaf shape
Pinus elliottii has two types of needles, one with two needles and one with three needles. The transverse section of each needle with a single needle is shown in Figure 1. Since the shapes of the needles of each needle are very similar, and the cutting planes between the different needle blades after folding are well coincided, in many studies, the cross-section of the closed blade is calculated as a true circle by default, but is it It is a true circle but it is not reported in the literature. Since the ratio of diameters in any two directions of a perfect circle is 1, the diameter ratio of the two directions of the blade cross-section is calculated and compared with 1, and the result of the t-test is used to determine whether the cross-section of each blade is a perfect circle. shape.
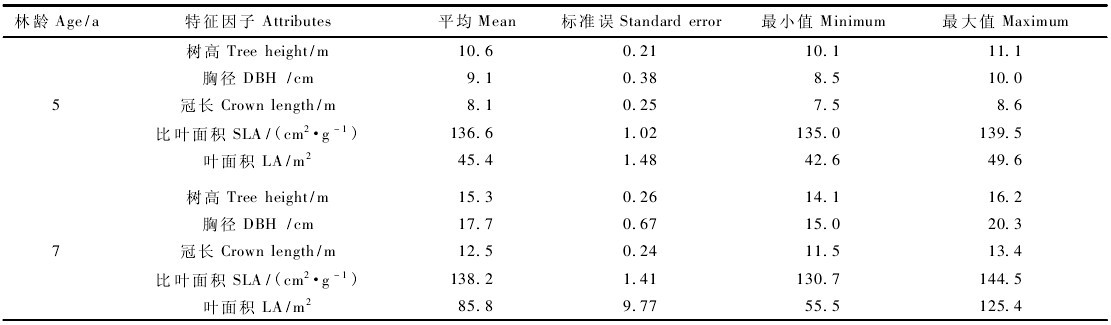

Two needles and one bunch of blades, the two selected diameter directions are the blade width (d) and thickness (h) direction, and the ratio R between d and 2h is directly calculated; three needles and one bunch of blades are equal to three needles to divide the circumference angle equally. The central angle corresponding to each needle is 120°. Calculate the radius based on the blade width (d) and its corresponding angle (120°) and calculate the radius with another measured radius (thickness h). Ratio R. Using the t-test to compare the difference between the ratios R and 1, the results showed that (Table 1), at a level of significance of 0.001, the two needles and one bundle of blades were folded together. The cross section was not perfectly circular, and the diameter in the thickness direction was significantly larger than the width. In the direction of diameter, the cross-section is closer to the ellipse; the cross-section of the three-needle bundle is basically a circle. If the two needles are bundled together, they are similarly regarded as a cylinder. The average diameter Dm is calculated by using the average of the blade width and 2 times the thickness. The same blade uses the drainage method to calculate the diameter Dv according to the volume, and the width between the blade and Dm The difference is denoted as Δ1, and the difference between Dm and Dv is denoted as Δ2. After calculation (Table 2), there is a difference of 2% to 10% between the blade width and the average diameter Dm, and the blade width is significantly smaller than the mean diameter of the blade. If the blade width is directly used as the cylinder diameter to calculate the blade surface area or the specific leaf area, it will inevitably bring the same degree of error to the result. If the parameter used is the blade thickness, the calculation result will be 2%~10% larger. In the sample surveyed, the average diameter and the diameter derived from the drainage method were similar, and most of them remained within 3%. Although statistically speaking, two needles and one bundle of leaves are not cylindrical after they are closed, but because the ellipse does not have a simple and practical perimeter calculation formula, in practice, it can be regarded as a cylinder to calculate the leaf area, but the diameter used The mean diameter Dm calculated using the blade width and 2 times the thickness must be larger if only one parameter of blade width or thickness is used instead.
2.2 Leaf length and leaf area
Due to differences in the understanding of the principle of contaminated radiation interception, the calculation of coniferous leaf area and specific leaf area has been divergent. This paper provides the calculation results of three kinds of leaf area for each blade for application in different occasions. One is the projected area of ​​the blade based on the product of the needle width (d) and length (l), and the other is each needle blade. The cylindrical surface area (ie, the area of ​​the outer surface of the cylinder that forms the cylinder when folded), and the third is the total surface area of ​​each needle blade. Since the three needles and needles are basically cylindrical after they are closed, the three calculation results for each needle blade basically only differ by a factor of two, and the two needles and one blade result in the difference in the relationship between the d and h of different beam blades. The difference in the three results is not constant. Find the average leaf area as shown in Table 3.
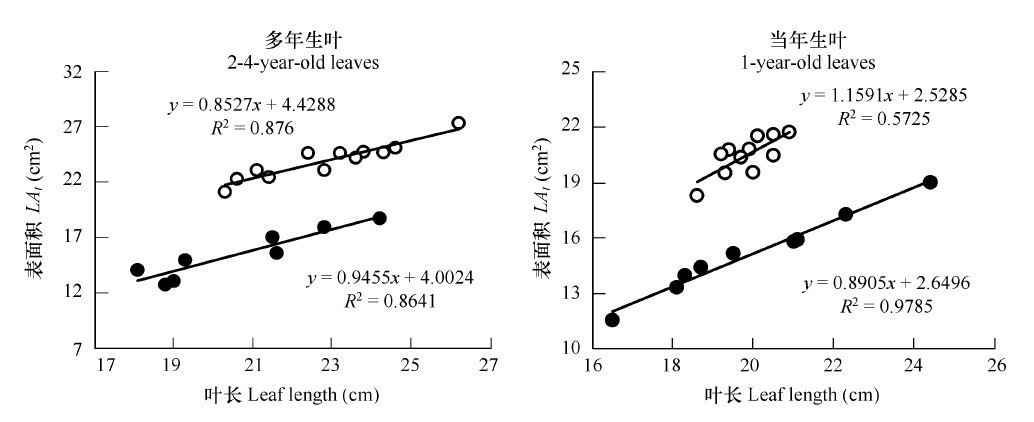
Among the three parameters of leaf length, leaf width and leaf thickness, the variation of leaf length was the largest, and the variation of leaf width and leaf thickness was relatively small. According to the existing data, the correlation between the length of the needle leaf and the total surface area was fitted. The result is shown in Fig. 2. The results of F-test showed that the relationship between the leaf length and leaf area of ​​the three-needle bunch was significant, and the other three correlations reached extremely significant levels. This shows that there is a significant correlation between the length of the coniferous leaves and the leaf area, and the leaf area can be directly estimated using the leaf length. If the sample size is increased and the applicable range of the equation is expanded, the deduced result will be more reliable. Similarly, the relationship between the projected area, the area of ​​the cylindrical surface and the leaf length can also be calculated according to the same method. The reason for the relatively poor correlation of the three-needle bundles is that the range of leaf length is relatively concentrated and the difference in leaf length is small, which has a certain influence on the fitting effect of the function.
2.3 Specific leaf area
The specific leaf area is the leaf area per unit dry weight leaf. When the leaves grew to August, the leaf morphology, such as leaf length, width, and thickness, and the perennial leaves were all comparable (Table 3), but there was a large difference in water content between the two (perennial leaf dry matter rate was 39. • 3%, when the leaves were 34.6%, which will cause the difference between the leaf and perennial leaves than the leaf area. The projected specific leaf area, the specific area of ​​the cylindrical surface, and the specific surface area were calculated using the dry weight of each needle and the three leaf area data as shown in Table 4. It can be seen that, for any of the three specific leaf areas, the specific leaf area of ​​the leaves of the same type in the current year is larger than that of the perennial leaf, and the shape of the leaves is not much different, indicating that this difference is partly due to the difference in water content. caused. The number of needle projections of different needles is larger than that of the leaf area with three needles, and the cylindrical surface is the opposite of the leaf area. The two needles are larger. This is because when the diameter of the cylinder increases, the mass increases in multiples of the square, and in a certain range of diameters, the increase in the projected area due to the increase in the number of coniferous leaves is greater than the increase in weight, and the increase in the external surface area of ​​the cylinder. Less than weight increments. The specific surface area is affected by the area of ​​the outer surface of the cylinder and the area of ​​the longitudinal section of each needle at the same time, showing the same pattern as the area ratio of the projection.
At present, there have been no reports on the proportion of two needles and three needles of needles of Pinus elliottii. In the current survey of 10 trees of 107 trees in March 2005, there were 3522 bundles of three needles and three needles. A bunch of 26097 bundles, the ratio between the two is 1.35 (or 57.45% and 42.55% each). Based on the average weight of two- and three-needle bunches of the year (0.123 g and 0.153 g, respectively), the dry weight ratio of the two leaves in the plot was 1.09 (or 52.15% and 47.85% respectively). Combining the specific leaf area of ​​each type of needles, the average leaf projection ratio leaf area, cylindrical surface specific leaf area, and specific surface area values ​​of 44.48 cm2/g, 62.80 cm2/g, and 111.27 cm2/g, respectively, were calculated. 51.01 cm2/g, 72.81 cm2/g, and 128.20 cm2/g.
2.4 Leaf area index
Based on the data obtained from the harvesting, the correlations between the base diameter (d) of branches of Pinus elliottii and biomass of shoots, diameter (D) of single wood, tree height (H) and biomass of individual wood were fitted. The former was d3. The linear function of the independent variable has the best fitting effect, while the latter has the best fitting function based on the power function with D2H as the independent variable. The equation with the highest correlation coefficient is shown in Figure 3. According to the regression equation and sample survey data between the DBH, tree height and leaf biomass of single tree, we calculated that there were 601.4kg of pine dry matter in two 20m×20m plots, ie 752g per square meter. The percentage of leaf biomass and perennial leaf biomass in the 156 shoots surveyed was 53.5% and 46.5%, respectively. The ratio between the two values ​​was 1.15, and the standard deviation was 0.15. The perennial leaf biomass, perennial leaf contribution 349.7g, the year contributed 402.3g. According to the specific leaf area of ​​each type of leaf, it can be calculated. If calculated according to the projection ratio leaf area, the average projected leaf area index of the two wetland sample plots is 3.61; if calculated according to the cylindrical surface specific leaf area, the cylindrical leaf area index is 5.12; calculated as half of the specific surface area, the result is 4.52.
3 Conclusions and discussions
3.1 Most of the calculation of the area of ​​coniferous leaves and leaves is to consider the coniferous cylinder as a cylinder. From the comparison of the width and the thickness of the leaf, the cross section of each coniferous leaf of the pine needles of the two needles is not a semicircle. Not a part of the semicircle (if it is, from the comparison of width and thickness, the surface of the blade will form an excellent arc, and the two blades together will form an “8†shape in cross section, but the actual situation is not the case), but When the result calculated by the cylinder is within 3% of the actual result, two needles and one leaf can be calculated as a cylinder in the actual calculation. Calculating the diameter of a cylinder by using only one of the width or thickness may give a large error to the result. The cross-section of the three-needle bundles can form a good circle.
In order to more accurately determine the shape of the cross-section of a single-needle blade, the author further validated the narrative of the previous leaf shape using the data obtained by the freehand slice scanning method. Using image processing software to measure the scanned image to obtain the transverse section parameters of the blade, as shown in Table 5. The average diameter of two blades and one blade is averagely obtained from the blade width and the double blade thickness, and the average diameter of the three-needle blade is the measurement of the two outermost sides. Radius measurements are averaged. The length of the semicircular arc (2.374 mm) calculated from the average diameter of two blades and the actual measured arc length of 2.439 mm and the diameter (1.859 mm and 1.864 mm, respectively) calculated using the blade width or blade thickness are not different. Large, and according to the measurement of the two radius and blade width calculated by the corresponding width of the central angle of 120.7 degrees, and 120 degrees almost no difference, further shows that the three needles after a bunch of blades can indeed be viewed as a cylinder.
3.2 When calculating the leaf area index of broad-leaved trees or crops, the leaf area is calculated based on the length and breadth of the leaves. The methods for calculating the leaf area are based on the leaf length (L) calculation (LA=f(L)) and according to the length of leaves (D). ) product calculation (LA = f (LD)) and so on. From the results, there is also a good correlation between the leaf length and leaf area of ​​S. elliottii. After establishing a regression equation with a large enough sample size, we can use the leaf length of S. pine to estimate the area of ​​single leaf.
3.3 There is a certain difference between leaf areas of perennial and current years, leaves of two needles and one leaf of three needles, which should be considered separately in the actual calculation. Otherwise, the results may bring greater errors. According to the weight ratio of two needles and three needles per leaf (1.09), the ratio of the current year's leaf to the perennial leaf (1.14), the average projection ratio of the wetted pine to the leaf area and the cylindrical surface can be calculated according to the field survey conducted in this experiment. Specific leaf area and specific surface area were 47.96 cm2/g, 68.13 cm2/g, and 120.29 cm2/g, respectively. Combining the equation of breast diameter, tree height and leaf biomass (FBS=0.0052(D2H)0.8529), the DBH, tree height, LAp, LAc and total surface area of ​​wetted pine were obtained. The correlation equations between (LAt) are LAp=0.0249(D2H)0.8529, LAc=0.0354(D2H)0.8529, LAt=0.0626(D2H)0.8529, respectively.
3.4 When different authors reported the index of the leaf area of ​​needles, some were based on the projection plane of the blade, some were based on the total surface of the blade, some were based on half surfaces, and others did not indicate which kind of area based on the leaves, and were given to different documents. The comparison of leaf area causes inconvenience and confusion, so Gower et al. proposed using the hemisurface area (HSA) to calculate the leaf area index of coniferous forests. This paper provides three kinds of leaf area indices. From the results obtained, there are more differences between the three leaf area indices, and both are larger than the results obtained with the portable leaf area meter (effective leaf area index is 2.40). The reason may be that the portable leaf area meter measures the effective leaf area index, and the effective leaf area index is obtained using the instrument to measure the clearance rate, and the value itself is smaller than the actual leaf area index. In addition, the maximum leaf area index value of S. elliottii is calculated in this paper, and the distribution of the blade and leaf inclination angles in reality often makes the value measured by the instrument small.
Heavy Duty Christmas Tree Disposable Bag won't rip or puncture!! Tear & Puncture Resistant.
Christmas Tree Removal Bag is the perfect solution for disposing your tree after the holidays.
We support customization to facilitate you to sell on amazon or locally.
christmas tree disposable bag,christmas tree trash bag,christmas tree cover bag
Dongguan Yalan Packing Materials Co., Ltd. , https://www.yalanpack.com
![<?echo $_SERVER['SERVER_NAME'];?>](/template/twentyseventeen/skin/images/header.jpg)