Using Lagrangian Relaxation to Solve the Problem of Economical Load Distribution in SIS

Solving the problem of economical distribution of load can bring huge economic benefits to power generation companies, and it is one of the key issues to be solved in SIS. Before the bidding, power companies in the market must measure the cost of the power generation company by repeatedly solving the problem of load economic distribution. After bidding, the bidding power must be allocated to each unit by solving the problem of load economic distribution. There are many methods to solve the problem of economical distribution of loads, such as Lagrangian relaxation method and dynamic programming method, and artificial intelligence methods such as opacity optimization algorithm and genetic algorithm. Dynamic programming method can easily lead to "dimensional disasters". The opacity optimization methods and genetic algorithms are time-consuming to solve, and strongly depend on the selection of various parameters in a specific solution. The traditional Lagrangian relaxation method uses the Lagrangian multiplier to establish the augmented objective function, and determines the active power of each unit according to the equal-rate microincrease rate and the Kuhn-Tucker condition. However, this method requires the unit's power consumption characteristics. The curve increases monotonically. In this paper, Lagrangian relaxation method is used. After Lagrange multipliers are used to relax the load constraints of the system, the obtained augmented objective function is not directly solved. Instead, the obtained Lagrangian function is first decomposed into An upper and lower level optimization problem is then solved separately. This not only does not require monotonic increase of the consumption characteristic curve, but also guarantees the rapidity and effectiveness of the algorithm.

I. Mathematical model of economic distribution of the load When there are altogether one set of units requiring economic distribution, the mathematical model of the economic distribution of the load is described as follows: Since the real-time load economic allocation problem is to be solved in the SIS, in the specific solution process, there are For the i-th unit generating power for a period of time, Pmini is the minimum generating power of the i-th unit, Pmaxi is the maximum generating power of the i-th generating unit, and ΔPi is the climbing constraint of the i-th unit.

Second, the principle of Lagrangian relaxation algorithm and its implementation steps In the Lagrange relaxation method to solve the problem of economic distribution of the load, the Lagrange multiplier is first used to relax the load constraints of the system to obtain the Lagrangian function: The Lagrangian relaxation algorithm flow is shown in Figure 1. Third, the actual application of a power plant 4 units of the actual operating parameters are shown in Table 1, the total power generation constraint Pd = 820MW. In order to demonstrate the effectiveness of the algorithm, the same set of data was solved using Lagrangian relaxation method, mixed oil optimization algorithm and genetic algorithm. The simulation shows that the Lagrangian relaxation method has a significantly faster solution speed, and the result is superior to the chaos optimization algorithm and the genetic algorithm (Table 2). When using chaos optimization algorithm and genetic algorithm, in order to guarantee the fast convergence of the algorithm, this paper will convert the original problem into the following form.

Objective function: Power generation constraints: (2) The genetic algorithm uses a real-coded form. The initial population is 50, the crossover probability is 0.5, and the mutation probability is 0.4.

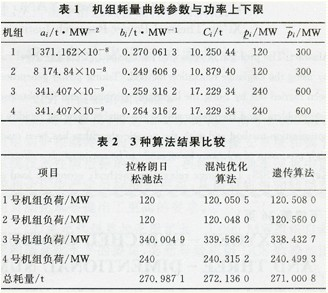
IV. CONCLUSION In this paper, Lagrange relaxation method is used to solve the problem of economical load distribution of SIS in power system. The simulation results show that the Lagrangian relaxation method has a simple search speed and provides an effective means for solving the problem of economic allocation of load in SIS. Lagrangian relaxation method not only can be used in power plant SIS, but also can be used in many issues such as load distribution in the electricity market, and has broad application prospects.

Features of Pharmacy Stainless Steel Filter Press:
1.Short working cycle and high efficiency.
2.Big capacity. Unique plate design makes filtrate discharge more smoothly to make higher processing capacity. 
3.Good filtering performance. Our Filter Press can endure higher feeding pressure, so that get lowest cake moisture. 
4.Low running cost. According to CE standard, our filter press has remarkable performance to decrease the running cost.
5. Filter Plate are made of reinforced polypropylene with features of high strength, corrosion resistance, nontoxic and odorless.
6.According to your material we will recommend special Filter Cloth, which can improving the filtering accuracy and efficiency . 
7.Main beam material is Q235B/Q345B, with sand blasting processing. 
8.Hydraulic station adopt ABB motor ensure stable performance. 
9.Hydraulic squeezing ensures no leakage to avoid secondary pollution.
10.Cabinet elements adopts international famous brands: Siemens Schneider etc. 

Pharmacy Stainless Steel Filter Press Photo:

 Features of Pharmacy Stainless Steel Filter Parameter:

Model	TG20/630-30U	TG30/630-30U	TG40/630-30U
Filter Area	20m2	30 m2	40 m2
Inside casing size	630*630 mm
Filter cake thickness	30 mm
Filtering board `s quantity	24 Pcs	37 Pcs	49 Pcs
Volume of filter casing	298 L	453 L	595 L
Pressure of cylinder	20-22
Machine size	3210*1150*1110 mm	3860*1150*1110mm	4470*1150*1110 mm
Weight	1870 kg	2170 kg	2440 kg

Pharmacy Stainless Steel Filter Press

Steel Plate Filter Press,Mechanical Portable Filter Press,Beer Filter Press For Olive,Wine Making Filter Press

Hebei TianGuan Filter Press Co., Ltd. , http://www.filterpressure.com